Sample base conversion worksheet
created in LaTeX.

LaTeX is amazing. And frustrating. And powerful. And frustrating.

This coming Fall semester, I will be teaching an introductory programming class for engineering students. To help them understand bits, bytes, integers, etc., is to have them practice base conversions between decimal, binary, and hexadecimal. I wanted to set this up in LaTeX, but the idea of typesetting all of those tables instantly gave me a headache. LaTeX should be able to help with the monotony, but convincing it of that will be an uphill climb.

Objectives

I want a single command that I can call, giving it two numbers (in decimal): (1.) the number on which to be shown in decimal, binary, and hexadecimal, and (2.) which of the 3 to not hide. The output should be a table in which every cell is a digit from the number of that base. The cells for binary and hexadecimal should line up so as to reinforce the relationship between them. The decimal cell, however, will not be split up, since it does not line up nicely with either binary or hexadecimal. Here is an example of what I want:

Lastly, because this is for student worksheets (and I also want to be able to produce an answer key), We need the ability to hide some of the output without losing the physical spacing. Here is an example of a base conversion in which only the binary is visible:

Defining the problem

We need to build 3 commands in LaTeX:

1. A command to get the specific digit for a number when in a particular base (up to base 16)
2. A command to selectively hide parts of the output (while preserving the physical layout spacing)
3. A command to output the table

Getting the correct digit for a given base.

This is perhaps the hardest requirement. I could not find a LaTeX command to perform this action, so I had to build it. The problem is, though, that LaTeX is not meant to be a programming language at all, so doing even simple calculations can be cumbersome, and there are significant limitations on what you can do.

We will use 3 packages: fp, ifthen, and fmtcount. fp is limited on the range of numbers that it can represent, but it has a larger range than the common alternative, pgfmath. Nevertheless, fp is sufficient for this use case (representing up to a 16-bit unsigned number).

\usepackage{fp}
\usepackage{ifthen}
\usepackage{fmtcount}
 
\newcommand{\getdigit}[3]{% number, digit, base
  \FPeval\power{round((#3)^(#2-1),0)}%
  \ifthenelse{#1<\power}{0}{%
    \FPeval\place{round((#3)^(#2),0)}%
    \FPeval\temp{round(#1-(trunc(#1/\place,0))*\place, 0)}%
    \ifthenelse{\power>\temp}{0}{%
      \FPeval\temp{trunc(\temp/\place*(#3),0)}%
      \Hexadecimalnum{\temp}%
    }%
  }%
}

This would be easier to understand if seen in a more readable language such as C++:

char getdigit(unsigned int number, unsigned int digit, unsigned int base) {
  unsigned int power = pow(base, digit - 1);
  if (number < power) {
    return '0';
  }
  else {
    unsigned int place = pow(base, digit);
    unsigned int temp = number - ((number / place) * place);
    if (power > temp) {
      return '0';
    }
    else {
      temp = (float)temp / place * base;
      char hex[] = "0123456789ABCDEF";
      return hex[temp];
    }
  }
}

Obviously, I would never use this approach in C++, but it serves the purpose to point out the difficulties of using fp in LaTeX. fp math is not exact. Even a simple exponent of whole numbers must be rounded in order to be correct. fp does not have the concept of integers (its name literally means "floating point"), so we must truncate and round everywhere. All of this means that the code is messy. To make it even less intuitive, the ifthen package does not understand <=, so you must test for the opposite (e.g., >). Lastly, there is no concept of returning early from a command, so all code must be constructed using the \ifthenelse command.

The main point, however, is that it works, and with that we can go to the next step.

Selectively hide parts of the table

When we say "selectively hide", we have a very specific requirement in mind. We want to have all of the physical space on the page preserved, but to not print it. It was suggested to me that I could simply set the text color to white and thereby hide the text, but because I may need to distribute the PDF to students, I don't want them to be able to copy-and-paste the whited-out answers. Luckily for us, there is a LaTeX package that will help us out: censor

The input for my command will have 3 parts: The text to either include or censor, and two numeric values. If the first numeric value is 0, then I will always show the text (because it is an example). If the two numeric values are equal, I will show the text, otherwise I will censor the text.

You may be asking, why go to all of this trouble to "censor" text? The answer is actually a feature of the censor package: by using a single command, I can "uncensor" everything, and thereby have an immediate answer key.

Here is the LaTeX code:

\usepackage{censor}
 
\newcommand{\censorifnotequal}[3]{% statement, val1, val2
  \ifthenelse{#2=0}{#1}{\ifthenelse{#2=#3}{#1}{\censor{#1}}}%
}

Create the table output

Creating a table programmatically is difficult in LaTeX. See the comments here to get an idea of the complexity involved. Because I am not a LaTeX guru, and I had already spent hours banging my head against my keyboard getting the above portions of code to work, I opted to hard-code the table inside the command. There are a few quirks, though, that I will mention. First, let's look at the bare table structure.

\def\colwidth{.42cm}
\newcommand{\baseconvertpractice}[2]{% number, # to not censor (1-3, or 0 for none)
  \renewcommand\arraystretch{2}
  \FPeval{\num}{#1}%
  \begin{tabular*}{\textwidth}{@{\extracolsep{\fill}}r|*{8}{>{\centering}p{\colwidth}|}|*{8}{>{\centering}p{\colwidth}|}@{}c@{}} \cline{2-17}%
  Decimal & \multicolumn{16}{ r| }{X} &\\ \cline{2-17}%
  Binary & X & X & X & X & X & X & X & X & X & X & X & X & X & X & X & X &\\ \cline{2-17}%
  Hexadecimal & \multicolumn{4}{c|}{X} &%
    \multicolumn{4}{c||}{X} &%
    \multicolumn{4}{c|}{X} &%
    \multicolumn{4}{c|}{X} &\\ \cline{2-17}%
  \end{tabular*}%
}

This produces the following output:

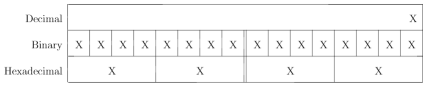
There are a few peculiarities with the layout. First of all, I put an empty column as the last column of the table. When left out, it produces errors and will not compile. I believe that this is a bug in the LaTeX compiler, so my workaround is to add the empty column. Second, I had problems with the column spacing being different if it contained a 0 or a 1, so I chose a size measurement to use explicitly (\colwidth, change as needed). Lastly, I had problems with the digits having a weird centering, so I had to use a more complex column declaration method. In the end, though, the output is nice.

Now for the final form, complete with optionally censored rows:

\def\colwidth{.42cm}
\newcommand{\baseconvertpractice}[2]{% number, # to not censor (1-3, or 0 for none)
  \renewcommand\arraystretch{2}
  \FPeval{\num}{#1}%
  \begin{tabular*}{\textwidth}{@{\extracolsep{\fill}}r|*{8}{>{\centering}p{\colwidth}|}|*{8}{>{\centering}p{\colwidth}|}@{}c@{}} \cline{2-17}%
  Decimal & \multicolumn{16}{ r| }{\censorifnotequal{\num}{#2}{1}} &\\ \cline{2-17}%
  Binary & \censorifnotequal{\getdigit{\num}{16}{2}}{#2}{2} &%
  \censorifnotequal{\getdigit{\num}{15}{2}}{#2}{2} &%
  \censorifnotequal{\getdigit{\num}{14}{2}}{#2}{2} &%
  \censorifnotequal{\getdigit{\num}{13}{2}}{#2}{2} &%
  \censorifnotequal{\getdigit{\num}{12}{2}}{#2}{2} &%
  \censorifnotequal{\getdigit{\num}{11}{2}}{#2}{2} &%
  \censorifnotequal{\getdigit{\num}{10}{2}}{#2}{2} &%
  \censorifnotequal{\getdigit{\num}{9}{2}}{#2}{2} &%
  \censorifnotequal{\getdigit{\num}{8}{2}}{#2}{2} &%
  \censorifnotequal{\getdigit{\num}{7}{2}}{#2}{2} &%
  \censorifnotequal{\getdigit{\num}{6}{2}}{#2}{2} &%
  \censorifnotequal{\getdigit{\num}{5}{2}}{#2}{2} &%
  \censorifnotequal{\getdigit{\num}{4}{2}}{#2}{2} &%
  \censorifnotequal{\getdigit{\num}{3}{2}}{#2}{2} &%
  \censorifnotequal{\getdigit{\num}{2}{2}}{#2}{2} &%
  \censorifnotequal{\getdigit{\num}{1}{2}}{#2}{2} &\\ \cline{2-17}%
  Hexadecimal & \multicolumn{4}{c|}{\censorifnotequal{\getdigit{\num}{4}{16}}{#2}{3}} &%
    \multicolumn{4}{c||}{\censorifnotequal{\getdigit{\num}{3}{16}}{#2}{3}} &%
    \multicolumn{4}{c|}{\censorifnotequal{\getdigit{\num}{2}{16}}{#2}{3}} &%
    \multicolumn{4}{c|}{\censorifnotequal{\getdigit{\num}{1}{16}}{#2}{3}} &\\ \cline{2-17}%
  \end{tabular*}%
}

This can be called in the following manner: \baseconvertpractice{42}{0}, in which 42 is the number that I want to be the answer, and  0 says that I don't want anything censored. If I put a 2 as the final argument instead, it would only include the binary but leave out the decimal and hexadecimal. Finally, from the censor package, the commands \StopCensoring and \RestartCensoring can be used to disable and reenable the censor behavior.

You may notice that censor, by default, puts a black box in place of the text. By adding the \censorruleheight=0ex command, there will be no black box at all, just the white space.

Conclusion

Hopefully this bit of LaTeX code will be beneficial to someone. For now, I'm on to creating the next homework assignment!