Taxonomy Term Tree Widget
Image from drupal.org

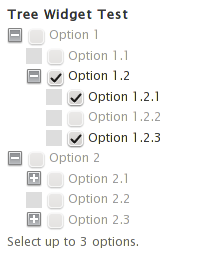
Taxonomy is a great tool in Drupal for categorizing information, unfortunately it is not often very "pretty" for the end user to interact with. Taxonomy Term Tree Widget addresses this deficiency by generating a pleasant, familiar tree structure from the target vocabulary's terms and their corresponding hierarchies. There is one problem, however, and that is that it is very difficult to filter the visible terms programmatically. The list can be filtered using a view (a setting accessible in the widget configuration form) however such a simplistic approach may not be flexible enough for most applications.

A Two-Pronged Attack

In order to address this problem, we need to approach it on different levels depending on how the data needs to be handled. First of all, there is the question of whether the tree should be visible at all. If the tree should be hidden and yet you do not want for the values to be erased when the entity is saved, then you must simply unset() the appropriate element inside the hook_form_FORM_ID_alter(). If you want to show some but not all of the tree, then you will have to get more creative. Beware, however, that removing fields in the way described in the remainder of this post will result in the removed fields not being retained at all when the form is submitted. If that is acceptable to you, then this method should work out fine.

Adding a #pre-render Directive to the Form

/**
 * Implements hook_form_BASE_FORM_ID_alter().
 */
function MODULENAME_form_ID_alter(&$form, &$form_state, $form_id) {
  $form['#pre_render'][] = 'MODULENAME_form_prerender_tree_prune';
}

In this code, we have simply added a hook to our module (MODULENAME) for a form with a particular form ID. There are several reasons as to why we cannot hide the tree elements here (namely, the tree has not been generated yet), so the pruning will have to take place in a separate pre-render function that we have called MODULENAME_form_prerender_tree_prune. The name of this pre-render function is up to us, so rename it however you choose.

Performing the Tree Pruning

To be perfectly honest, this part of the code is hairy. The array structure at this point is very complex, and it is possible that things won't be where you expect them to be. I'll give you the code first and then talk you through it.

/**
 * Pre-render function (added in MODULENAME_form_ID_alter) which will
 * prune undesired terms.  At this point, if a term is not visible, it
 * will not be saved when the form is submitted.
 */
function MODULENAME_form_prerender_tree_prune($element) {
  // Array of term ids (actually, the keys are the tids and the
  // associated values can be anything) that should not be removed.
  $tids_to_keep = array(
    1 => 1,
    2 => 2,
    5 => 5,
  );
 
  // Perform the recursive pruning.
  // Replace FIELD_NAME with the appropriate information.
  MODULENAME_tree_prune_recursive($element['FIELD_NAME'][LANGUAGE_NONE][0], $tids_to_keep);
  return $element;
}
 
/**
 * Recursive function used by MODULENAME_form_prerender_tree_prune()
 * to prune the terms visible in the taxonomy select tree.
 */
function MODULENAME_tree_prune_recursive(&$element, &$allowed) {
  if (is_array($element)) {
    if (isset($element['#type']) && $element['#type'] == 'checkbox_tree_level') {
      foreach ($element as $delta => &$val) {
        if (isset($val['#type']) && $val['#type'] == 'checkbox_tree_item') {
          if (!isset($allowed[$delta])) {
            // Remove the checkbox
            unset($element[$delta]);
          }
          else {
            // Item is allowed, perform the check on the children.
            if (isset($val[$delta . '-children'])) {
              MODULENAME_tree_prune_recursive($val[$delta . '-children'], $allowed);
            }
          }
        }
      }
    }
  }
}

The first order of business is to define an array of tids (taxonomy term ids) that we want to keep. The tids are used for both the key and values in the $tids_to_keep array, although the key is the important part of the code since it is more efficient to use it in this manner. The second statement in the function invokes a recursive routine to prune out the unwanted branches of the tree. Notice how far into the array we reach; you should probably double-check the structure of the $element array to ensure that the field is where you think it is. In fact, if you are using field groups or any other special treatment of fields then the data is probably nested further into the $element array than it is when accessing it in the MODULENAME_form_ID_alter(). The important thing is that the array that gets passed in to the recursive function should have a #type of checkbox_tree_level, otherwise the function will be ineffective. It's sticky, but that's why we have dsm()!

The recursive function MODULENAME_tree_prune_recursive() is ugly but straightforward. It traverses down into the array using the expected structure and weeds out the undesired terms. It should be noted that in this implementation, if a parent term is removed, all child terms will be removed as well. I did not need more complex action so I did not write it.

Wrap-Up

While not the prettiest solution, this bit of code allows us to customize which terms are presented to the user, all without having to hack the original module. This implementation is fast and, in my situation, solves a very complex problem of who can access which term in a taxonomy and when, all the while retaining the beautiful tree interface of the original module. It should be noted that, in my setup, I have not enabled any of the ajax functionality of the module, and I don't know how it would respond to this enhancement, so caveat emptor. Otherwise, let me know if this bit of code worked for you, or if you have found a different way to get this accomplished.